Suppose you want to make a muon-antimuon pair (μ) by colliding and annihilating a positron and an electron.
|
|
(1) |
|---|
The (muon) μ particles are each about 200 times the mass of an electron, so most of the kinetic energy of the electron and positron must be used to create them.
The positron e+ could be fired at a stationary electron (in practice the electron would be bound in an atom with a kinetic energy of a few eV, which is negligible compared with the high energies involved in Particle Physics).
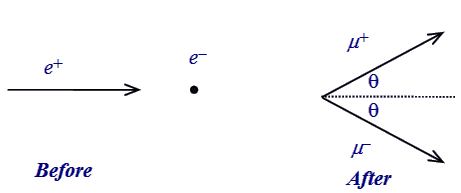
The incident positron (e+) has
momentum pe and total energy
Ee and collides with a stationary
electron (e−) thereby annihilating
to produce a 'virtual photon'. The virtual photon materialises into
a new e+ and
e− pair or any other heavier particle-antiparticle pair,
such as μ+ and
μ−, provided sufficient energy
is available. The μ+ and
μ− pair must have total momentum
equal to pe in order to conserve
momentum in the collision.
Combining the relativistic energy and the momentum conservation equations
yields the equation below:
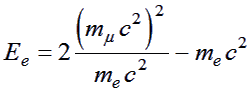 |
(2) |
|---|
This is the total energy of the positron at which particles are produced with the least possible momentum, so it is, therefore, the threshold energy.
Put the masses into this equation and calculate (use Excel etc. or a calculator) the threshold total energy for pair production by positrons hitting a stationary target:
| Particle | Mass in MeV/c2 | Colour Key |
| electron (e+/e−) | 0.511 | |
| muon (μ+/μ−) | 105.7 | |
| pion (π+/π−) | 139.6 | |
| kaon (K+/K−) | 493.7 | |
| proton (p+/p−) | 938.3 |
The actual type of particle-antiparticle pair created is random once you are above the threshold energy. Thus you might simply create a new electron-positron pair even though you have enough energy to make muons. You need to repeat the experiment a few times before increasing the beam energy.
Now run the animation and test your prediction for the threshold energy.
