Decay Modes and Branching Ratios
The aim of the simulation is for you to identify, using the information on the previous page, the different decay modes and then to measure the various branching ratios of the Higgs boson for yourself. To do this, below is how to identify each of the decay modes of the Higgs boson once you have identified each of the particles using the information on the previous page.
The Decay Modes
The Higgs boson has four main decay channels with the corresponding branching ratio (reference):
- H → γγ (Higgs boson to two photons 0.229%)
- H → ZZ → LLLL (Higgs boson to two Z bosons to four leptons 0.0131%)
- H → ττ̅ (Higgs to a tau lepton and an anti-tau lepton 6.28%)
- H → bb̅ (Higgs boson to a b-quark and an anti-b-quark 56.9%)
How to identify them?
Within this simulation, only the four decay channels above are presented. To identify them there are several techniques which physicists at CERN use to identify each individual of the channels.
Identifying H → γγ (Higgs boson to two photons)
As discussed on the previous page, a photon will deposit energy only in the electromagnetic calorimeter (the innermost ring) and will leave no track. A Higgs boson to two photons is, therefore, the cleanest decay mode to identify as there shall only be the two photons to identify. Due to how clean this signal is, it is this decay channel that was originally used to discover the Higgs boson despite the low branching ratio of 0.229%.
Identifying H → ZZ → LLLL (Higgs boson to a pair of Z bosons to four leptons)
This decay mode is trickier as the end product which you identify can vary. The Higgs boson will decay into a pair of Z bosons, each of which will decay into a pair of leptons. To maintain conservation laws, the two leptons in the pair must be the same particle, but each pair can be different to the other, or the same. Therefore, ignoring the tau lepton, the following combinations are valid: four electrons, four muons and two electrons and two muons.
To identify electrons, you are after energy only in the electromagnetic calorimeter and track. To identify muons, look for energy in the outermost ring (the Muon spectrometer) and a track too. To identify this channel, therefore, look for pairs of electrons and muons, looking for four leptons in total whose energy will add to that of the Higgs boson's energy.
Identifying H → ττ̅ (Higgs to a tau lepton and an anti-tau lepton)
Taus are possibly the trickiest to identify due to a very short lifetime of 2.9 x 10-13 s and a high mass, resulting in the tau decaying into electrons, muons and pions. You will never see a tau itself in a detector due to their very short lifetime, only particles that a tau lepton will decay into. Tau leptons decay into electrons, muons and pions. If a tau decays, the lepton number (the amount of "tauness") has to be conserved which is done by producing a tau neutrino. If an electron or muon is created, then there must also be the corresponding electron (or muon) flavoured anti-neutrino to preserve lepton number.
Two combinations of pions can be produced, three pions with one of a different charge to balance the charge from the tau, or one pion with the same charge as that of the tau.
Therefore, to identify a tau decay, you are looking for an electron, a muon, a single pion or three pions along with one or two neutrinos. (The neutrinos will only be visible if the neutrino option is selected). Since neutrinos cannot be detected normally, you can tell if neutrinos are present due to missing energy - if you sum the energy of all the particles visible, it should equal the energy of the Higgs boson. Missing energy from this total indicates the presence of neutrinos.
The mass and momentum of the tau lepton also means that the decay products become a jet (multiple particles bunched up into a cone shape) resulting in some energy towers overlapping.
Identifying H → bb̅ (Higgs boson to a b-quark and anti-b-quark)
b-quarks have a mass of 4.2 GeV, over double the mass of a tau (1.77 GeV), and so will decay into more particles of more energy. Therefore, expect tight jets of 9-12 particles. The jets will consist of mostly pions but may also have pairs of electrons and muons too. A b-quark is identifiable by the volume of particles produced from hadronisation - if there are more than 8 particles on the screen, it must be a b-quark decaying!
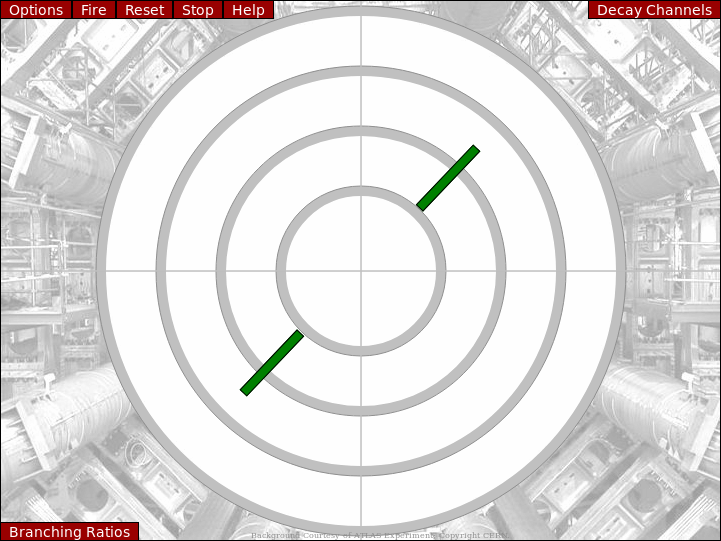 H → γγ
H → γγ

A Higgs boson decaying into two photons. The photons are identified by energy only in the ECAL and no tracks. The photons are created back to back, and if the Higgs boson has energy, boosted by that energy to bend towards eachother.
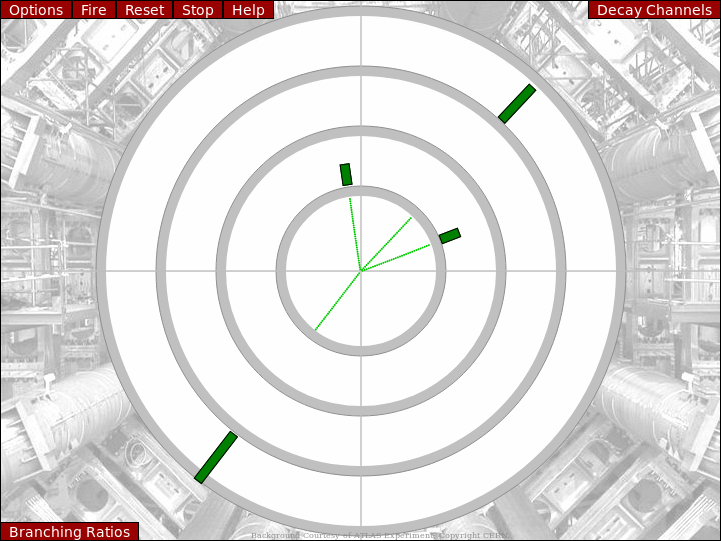 H → ZZ → llll
H → ZZ → llll

A Higgs boson decaying into two Z bosons, which each decay into a pair of electrons or muons. Electrons will only deposit energy in the ECAL, muons will only deposit energy in the Muon spectrometer and both particles will leave tracks.
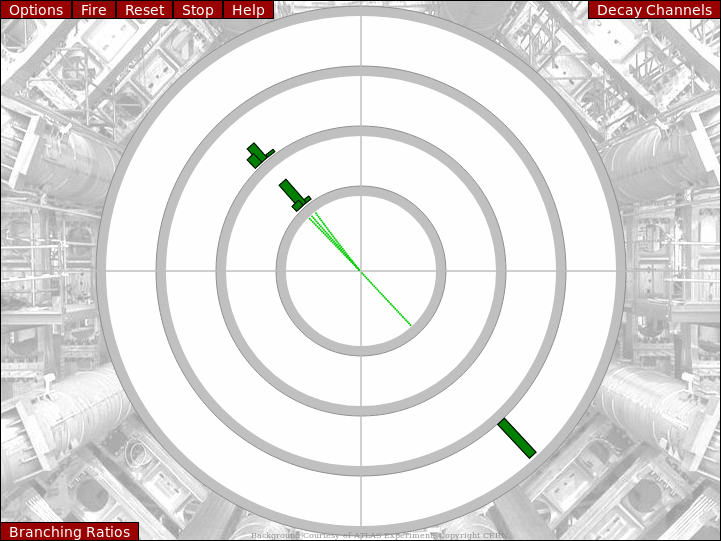 H → ττ̅
H → ττ̅

A Higgs boson decaying into a tau and an anti-tau lepton. The tau will then decay into
- an electron, an anti-electron neutrino and a tau neutrino
- a muon, an anti-muon neutrino and a tau neutrino
- a single pion and a tau neutrino
- three pions and a tau neutrino.
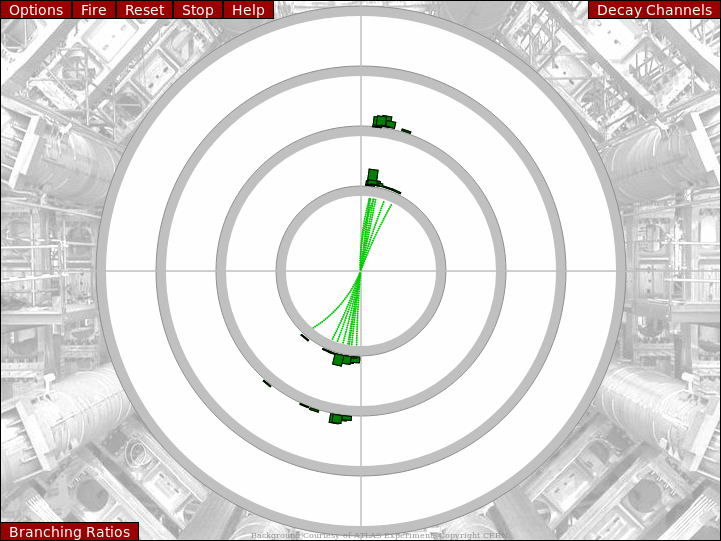 H → bb̅
H → bb̅

A Higgs boson decaying into two b-quarks where each b-quark quickly hadronises creating a shower of pions. Between 9 and 12 pions are produced per b-quark, and due to the momentum of the b-quark, the particles are boosted towards eachother forming a cone/jet of particles.
Branching Ratios
The Branching ratio is a percentage chance that a particle will decay a certain way. For example, the decay of a Higgs boson into two photons has a branching ratio of 0.229%, an incredibly low value, compared to the branching ratio of 56.9% for a Higgs to decay into two b-quarks. This tells us that a Higgs boson is much more likely to decay into b-quarks than photons. This ratio is directly measurable in experiments by observing how many times you see a Higgs boson decay into that combination of particles, and something that you can see for yourself within the following simulation.
Whilst a branching ratio might be high or low, this is not the only factor that affects whether or not you shall see it in a detector, some of the decay channels are more difficult to identify than others. For example, the channel of Higgs to two photons has a very low branching ratio and low probability of it occurring but the signal of only two photons that are produced back to back is very clear, a similar situation with two Z bosons going into two pairs of leptons. Because of their clear signal, it was a combination of H → ZZ → llll and H → γγ which was used to identify the Higgs boson originally. The H → bb̅ channel has a significantly higher branching ratio, but the volume of pions that have to be identified from hundreds of background collisions also creating pions makes it incredibly difficult to isolate and use accurately, similarly with the H → ττ̅.
Within this simulation, only four of the many decay modes are included and so the sum of the individual branching ratios of the four shown channels does not add up to 100%, it adds up to about 63.4%. To account for this, within the pie chart in the simulation is a branching ratio that accounts for the missing channels. This can be thought of as the target branching ratio which would apply to the simulation.
Acceptance times Efficiency
Alongside factors such as the clarity of a decay and the amount of background, you also have to consider mechanical factors of the detector as no detector is perfect e.g. the ATLAS detector cannot measure any particles that decay back along the beamline (the protons travel along and out of a beam to collide, any particles that go back into the beam are not measured as the equipment would affect how the protons behave). The range in which the detector can measure particles, whether it be due to the particle's momentum or direction, is called the acceptance.
The intrinsic efficiency is given by the fraction of events registered by the detector with respect to the number of events hitting the detector. This, therefore, takes into account various factors such as any background making it difficult to isolate a certain event, or issues with energy or momentum resolution within a detector. The total efficiency is given by multiplying the intrinsic efficiency by the acceptance, and this total efficiency represents how many of that particular event is detected compared to how often it occurs.
So open up the application and have a go!
Instructions on how to run the application:
- When ready, press the 'Fire' button in the top left corner and a particle collision will occur.
- Using the above information, try to figure out what particles are being shown. From this, you can determine which decay channel you are seeing the Higgs boson decay via (for a list, see the options in the top right corner of the screen).
- Once you know which decay it is, click on the corresponding decay in the top right corner, if correct it will then add this to the decay channels that you have seen and identified! Well done! If you select an incorrect decay channel, then try and identify the particles again. Remember, a photon has no charge and hence leaves no track, electrons will have a track and appear in the ECAL, Pions will appear in the ECAL and HCAL, and Muons will only appear in the Muon ring.
- Click the 'Fire' button again and identify some more decay channels. As you identify the channels, do not forget to select the correct option for it!
- As you identify the various decay channels, a pie chart is built in the bottom left showing the amount of each you have observed. This shows you how much this would be observed in real life (hence the difference in number).
- Once you have observed and identified 10 decays, an autofire button will be unlocked. Use this to see lots of events happen quickly so you can see the branching ratios of each decay channel.
